コンピューターの高性能化によって、多少乱暴な書き方をしたとしても十分なパフォーマンスを発揮してくれるようになったため、パフォーマンスは昔に比べてそれほど重視されなくなりました。
しかし、それに甘えていると、インスタンスを無用に増やしてランニングコストが掛かってしまったり、ユーザビリティを損なうケースも存在します。test環境では大丈夫だったけど、production環境では耐えきれなかった…ということもよくあります。
パフォーマンス起因でシステムが停止したり、hotfixを当てないといけないような状況に陥ったりしないためにも、ここで紹介する内容を是非意識して実装してみてください。
はじめに
本記事では、記事中で示すサンプルコードの言語としてJavaScriptを採用していますが、考え方自体はどの言語でも応用できます。他言語の読者に向けて、一部分かりづらい部分に関してコメント構文(//)による注釈を設けています。
対象の読者
本稿は、パフォーマンスチューニングの必要があるけれど、どこから手をつけていいか分からない!という入門者に向けて書いています。そのため、記事ではあくまで指針を示すに留め、詳細なチューニング方法などは記載しておりません。もしご質問がありましたら、twitterや記事のコメント欄に頂ければ、個別に返信させて頂きます。
オーダ記法について
本稿では、コストの表現方法として、オーダ記法を使用します。オーダ記法とは、O(n)のような書き方をするもので、ざっくり言えば、nを計算対象(例えば、リストのlength)だとしたときに、どれくらいの計算量が必要かを表すものです。オーダ記法についてご存知の方は、本項目を飛ばして頂いて構いません。
仮に、n件のlengthを持つデータリスト定数DATA_LISTがあるとします。
for(let data of DATA_LIST){ // 変数dataにDATA_LISTの内容をひとつずつ代入しながら最後までループする構文です。
// do something.
}
上記コードはDATA_LISTの内容を全て走査し、途中終了する条件もないため、計算量はリストのlengthと同じ、nです。これを本稿ではO(n)と表現します。
次に、単純なnested loopを書いてみます。
for(let data of DATA_LIST){
for(let data2 of DATA_LIST){
// do something.
}
}
これは、n×n、すなわち、n^2の計算が行われます。この場合、O(n^2)と表現します。
本稿では、いずれも「時間計算量」としてオーダ記法を用います。「空間計算量」、すなわち、メモリ使用量については本稿の本質から外れるため、言及しません。
基本的な考え方
プログラムのパフォーマンスチューニングは、大別すると3種類のアプローチ方法が存在します。
- プログラムの処理自体を高速化する方法
- 「事前処理」を行うことで、結果的に高速化を行う方法
- 並列化による方法
いずれも、効果のあるケースは変わってきます。本稿では、どういった事例に対して、どういった対策が有効なのか、について触れていきます。
パフォーマンスに影響を与えるもの
パフォーマンスに与える影響としては、計算量以外にも重要な要素があります。たとえば、ファイルの入出力はDISKの速度に依存しますし、外部APIコールは、「そのAPI自体のパフォーマンス」に依存します。言語仕様としてそもそも「使うだけで遅い」という機能もあります。これらを頭に入れておくことで、ボトルネックを探る手助けになります。ここでは、特にボトルネックになりやすい、代表的なものについて触れていきます。
計算量
無駄な計算は、それだけでパフォーマンスの悪化を招きます。以下は、nを引数にとり、n番目のフィボナッチ数を返す、単純な計算プログラムです。
function fib(n){
let prev = 0;
let current = 1;
for(let i = 0; i < n; i++){
const next = current + prev;
prev = current
current = next;
}
return current;
}
これは、1回のみ実行する場合なら想定通りに動くし、何の問題もないでしょう。しかし、「1〜20までの全てのフィボナッチ数を計算して出力する」という要件が加わったとき、愚直にやると以下のようになります。
for (let i = 1; i <= 20; i++){ // 20回繰り返す
console.log(fib(i));
}
このコードでは、全てのfib()関数の呼び出しにおいて、フィボナッチ数を0から計算していることになります。本来、フィボナッチ数は、ひとつ前とその前の数値を単純にプラスしたものですから、その値を保存しておけば、再び計算しなくてもよいはずです。こういった無駄な計算を見つけ出すことはパフォーマンスチューニングの第一歩になります。
IOの速度
他のデバイスにアクセスするIO処理は、特に注意すべきです。特に機会が多いのはディスクアクセスです。今はSSDの普及によって高速化していますが、それでもメモリアクセスに比べると、数値にして100倍以上は遅くなります。
ネットワークを介した外部アクセス
WebAPIのコールはもちろんのこと、データベースやKVSへのアクセスもネットワークを介していることを忘れてはいけません。場合によっては、ネットワークの経路をより高速なものに変更することや、利用しているサービスの変更を検討することで大幅な改善が見込める場合もあります。
言語特性
一般論的に言えば、スクリプト(インタプリタ)言語はコンパイルが必要な言語と比べると低速である、と言われています。こういった言語特性についてよく知っておく必要があります。
たとえば、pythonには様々な実装があります。有名なのはcpythonですが、より高速なpypyという実装があります。しかし、pypyは高速ですが、cpythonと比べて起動が遅いなどのデメリットも目立ちます。
こういった言語や実装の特性をよく理解することで、より適したコーディングや、実装の選択が出来るようになります。
高コストな処理
インスタンスの生成などは高コストな処理であるとよく言われます。通常のパフォーマンスチューニングではあまり意識することは無いと思いますが、知識として持っておくと思わぬところで役に立つかもしれません。
後述しますが、ソートや二分探索などのアルゴリズムの計算量なども、基礎知識として身につけておくことをお勧めします。
実装時にパフォーマンスを気にすることは悪なのか?
しばしば、実装時にパフォーマンスを気にすることはあまり良い習慣ではないとされることもあります。
パフォーマンスチューニングは、可読性の悪化を伴うことも珍しくありませんし、気にして実装したコードが、実は全体からすればあまり意味が無く、より複雑になってしまっただけ、ということもよくあります。
しかし、実装時に計算量やボトルネックとなりそうな箇所を意識しておくのは悪いことではありません。あくまで、パフォーマンスを気にするあまり可読性が悪化したり、よくない影響をコードに落とすことを戒めたものなので、そうならない程度にパフォーマンスを気にすることは、むしろ良いことです。
パフォーマンスを気にするあまり、不要なコードを書いてしまわないようにだけ気をつけてください。
プロファイルする
パフォーマンスチューニングを行うにあたってまず大切なことは、現状を把握することです。どこが遅くなっているか、改善できる余地があるのか、また、過度にループが回っているところが無いかを確かめます。
コードの印象と、実際の処理時間は大きく乖離することも少なくはありません。リソース投資の優先順位を正しく把握するためにも、まずは現状把握を行うようにしましょう。
実行時間を計測する
任意のコード境界にタイマーを仕込み、実際に動かしてみて時間を計測するのは悪くない方法です。どこにどれくらいの時間が掛かっているかを把握でき、改善するとどの程度の効果を得られるかがわかります。
仮に、処理に10秒かかっている部分のパフォーマンスを改善したいとします。そこからは3種類のモジュールA,B,Cが呼ばれており、どれもコード上では時間がかかりそうな処理を行っているようです。しかし、実際に時間を計測すると以下のような結果になりました。
| モジュール | 処理に掛かった時間 |
|---|---|
| A | 1秒 |
| B | 2秒 |
| C | 7秒 |
この場合、モジュールAをいくら頑張って完璧にチューニングしたとしても、得られる最大の効果は1秒までです。対して、モジュールCは、例えば処理時間を50%に短縮できたなら、実に3.5秒もの時間短縮になります。
処理回数をカウントする
for文など、主要ループの最も深い部分の処理回数をカウントします。適切な関数に分けられていれば数えるのはそんなに難しい話ではありませんし、多くの場合は専用のプロファイラにこういった機能が搭載されていたりします。
処理すべきリストのlengthが1000であるにも関わらず、ループ回数が1000000回、などとなっていたら、明らかに怪しむべきところです。
無駄な計算を抑える
線形探索を削減する
線形探索のコストは、O(n)です。例えば、1000件のリストがあるとして、その中のオブジェクトをフィルタする必要があるとき、リストを全件走査する必要があります。JavaScriptなどで例えれば、Array.filterなどがそれに当たりそうです。
以下のようなプログラムをチューニングしてみましょう。ユーザーのリストから、ユーザーIDを用いてレコードを検索するプログラムです。
class Users{
users = [
{id: 1, name: "Alpha"},
{id: 2, name: "Bravo"},
{id: 3, name: "Charlie"},
{id: 4, name: "Delta"},
{id: 5, name: "Echo"},
];
findUserById(id){
let foundUser = null;
for(let user of this.users){
if(user.id === id){
foundUser = user;
}
}
return foundUser;
}
}
このコードには2つの問題があります。まず1つは、探索を途中で打ち切っていないこと。線形探索はO(n)の計算コストを要しますが、今回の「ユーザーID」のような、一意に定まるsymbolをキーとして探索するケースでは、ユーザーがみつかればそこで探索を打ち切っても構わないわけですから、その場で必ずbreakやreturnなどでループを打ち切るようにします。
この場合、最良値はリストの先頭にユーザーがいた場合でO(1)、最悪値はリストの末尾にユーザーがいた場合でO(n)となります。つまり、findUserByIdは、平均O(n/2)の計算量にまで削減できます。
しかし、まだやれることはあります。IDで一意にユーザーが特定できるということは、HashMapやDictとして表現できる、ということです。HashMap, Dictなどの構造にした場合は、探索コストはHashを計算するだけなので、常にO(1)となります。これらを踏まえて、チューニングしてみましょう。
class Users{
users = [
{id: 1, name: "Alpha"},
{id: 2, name: "Bravo"},
{id: 3, name: "Charlie"},
{id: 4, name: "Delta"},
{id: 5, name: "Echo"},
];
createUserByIdIndex(){
// ここでユーザーのdictを作るのにコストがO(n)かかるが、一度計算されたら再計算されないので、
// 何回findUserByIdを呼ばれたとしても、かかるコストは初回のO(n)のみ。
const userById = {};
for(let user of this.users){
userById[user.id] = user;
}
this._userById = userById;
}
findUserById(id){
if(!this._userById){
this.createUserByIdIndex();
}
return this._userById[id];
}
}
上記のプログラムを用いて、「ユーザーを10回検索する」という条件で比較してみます。
| プログラム | 初回計算コスト | 1回あたりの計算コスト | ×10 | 合計計算コスト |
|---|---|---|---|---|
| チューニング前 | 0 | 5 | 50 | 50 |
| チューニング後 | 5 | 1 | 10 | 15 |
大幅に計算量が削減されていることがわかります。
ネストループを削減する
上述した内容と似たような感じになりますが、以下の2つのデータセットを結合することを想定してみます。ECサイトにおいて、「どのユーザーのカートにどんな商品が入っているか」をリアルタイムで確認できる分析画面のようなものを想像してください。
users
| id | name |
|---|---|
| 1 | Alpha |
| 2 | Bravo |
| 3 | Charlie |
carts
| userId | itemName | quantity |
|---|---|---|
| 1 | Protein | 3 |
| 1 | Milk | 3 |
| 2 | Chicken | 1 |
| 2 | Water | 1 |
| 2 | Tea | 1 |
| 1 | Beef | 3 |
ユーザーは複数人いて、Cartの内容はuserId順に並んでいるわけではないから、ユーザー毎にCartの内容を走査し、合致する条件だけ抜き出してくれば良い、と考えてみます。
const userAndCarts = [];
for(let user of users){
const userAndCart = {user: user, cart: []}
for(let item of carts){
if(item.userId === user.id){
userAndCart.cart.push(item); // push()は、他言語ではappend, addなどと表現されます
}
}
}
return userAndCarts;
usersのlengthをn、cartsのlengthをmとすると、このコードの計算コストはO(n*m)となります。上記の例で言えば、usersは3、cartsは6のデータがありますので、O(18)と言えます。
このコードをチューニングするとしましょう。userAndCartsを作成するための計算コストはO(n+m)まで削減することができます。
// userId毎にカートを事前準備する
const cartByUserId = {};
for(let item of carts){
if(!(item.userId in cartByUserId)){
cartByUserId[item.userId] = []; // 該当のuserIdに要素が存在しなかったら空のリストを作成します
}
cartByUserId[item.userId].push(item);
}
const userAndCarts = [];
for(let user of users){
const cart = cartByUserId[user.id] || []; // 元のコードとふるまいを変えないため、要素がなければ代わりに空の配列を定義(|| []の部分)
const userAndCart = {user: user, cart: cart}
}
return userAndCarts;
このように、そもそもの計算量を削減することで、パフォーマンス向上を見込めることがあります。
アルゴリズムを見直す
複数のアルゴリズムを有するものでは、sortが最も思い浮かびやすいですが、listやmapなどのオブジェクトにもアルゴリズム(実装)が存在することをご存知でしょうか。プログラム特性によっては、このアルゴリズムを変えるだけで思わぬ効果を生むことがあります。
適切なアルゴリズムを選択する
Wikipediaのアルゴリズムページの中の、代表的なアルゴリズムにアルゴリズムの種類が羅列されています。すべて詳細に学習する必要はありません。各アルゴリズムの特性を知っておけば十分です。
一例として、有名な探索アルゴリズムの解説を行います。
Listなどの検索で通常使用されるアルゴリズムは、「線形探索(リニアサーチ)」といって、「条件に訪ね当たるまで先頭から末尾まで走査する」という、いたって単純なアルゴリズムです。
単純だからといって、悪いわけではありません。むしろ構造の制約が無い分、多くのケースに適しているアルゴリズムです。
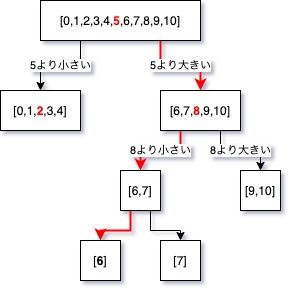
対して、有名なアルゴリズムとして、「二分探索(バイナリサーチ)」というものがあります。これは、予めソートされた配列に対して、中央点をピックアップし、対象が検索すべき値に対して大きいか小さいかによって、前(左側)を探索しにいくか、後ろ(右側)を探索しにいくかを判定し、またその中央をピックアップし、探しに行く、というアルゴリズムです。探索をしにいく毎に対象の配列の長さが半分になっていくのが特徴で、計算量はO(log n)となります。文章で書いてもわかりづらいので、例示すると、
TEST_DATA = [0,1,2,3,4,5,6,7,8,9,10]という配列があり、
EXPECTED = 6を探しに行くとします。
まず、TEST_DATAの中央値として5がピックアップされます。
EXPECTEDは5より大きいため、次なるテスト対象は、5より大きい部分、すなわち、
[6,7,8,9,10]となります。この中央の値をピックアップすると、「8」であることがわかります。
EXPECTEDは8より小さいため、次は[6,7]が次の検索対象であることがわかります。
[6,7]の中央の位置を特定することができません。この場合は、切り捨て・切り上げ・四捨五入などの処理を行って値を丸めます。
今回は切り捨てを行ってみることにします。つまり、[6,7]の中央の値を「6」としてピックアップします。
EXPECTEDは6と同じなので、配列中に6が存在することを確認でき、その要素の位置を特定できました。
勘の良い方なら既にお気づきかと思いますが、この「二分探索」は、検索対象の値がソート済みでなければ、誤った結果を生み出します。
例えば、[3,1,0,4,2]といった配列の場合で3を探したい場合を考えてみますと、中央の値が0となるため、二分探索は右の配列[4,2]から探しに行こうとしますが、実際に3の値が入っているのはそれより左の0番目に位置しています。これをそのまま実行すると、「値が見つからなかった」という結果になります。3という値は存在するわけですから、これは明らかに想定する結果ではありません。
二分探索は手軽で便利なアルゴリズムですが、こういった条件を全て整えた上で、という制約付きで高いパフォーマンスを生み出しています。
そうなると、二分探索のコストの他に、ソートのコストが加わってきますから、一概に二分探索が優れているとは言えません。コードによって、選択すべきアルゴリズムは変化します。
アルゴリズムは、その特性を理解して初めてパフォーマンスチューニングに使えるわけです。
キャッシュする
同じ計算結果を複数回使うことが想定される場合、その結果を保持(キャッシュ)しておくことは、多くの場合非常に有効です。実装はシンプルで、冒頭に例として挙げた、フィボナッチ数を計算するプログラムをキャッシュしてみることにします。
function fib(n){
let prev = 0;
let current = 1;
for(let i = 0; i < n; i++){
const next = current + prev;
prev = current
current = next;
}
return current;
}
class FibonacciCalculator{
constructor(){
this.cache = {};
}
calculate(n){
if (n in this.cache){ // nがキーとしてthis.cache(dictionary)に存在するか判定
return this.cache[n]; // 計算結果がキャッシュにあればそれを利用
}
const result = fib(n);
this.cache[n] = result; // 計算結果がキャッシュされていなければ、計算してキャッシュする
return result;
}
}
calculator = new FibonacciCalculator();
calculator.calculate(10);
calculator.calculate(10);
calculator.calculate(10); // 何回呼び出しても、実際に計算が行われるのは1回だけ
しかしこれにも、勿論気にしなければいけないことがあります。
キャッシュには、書き込み・キーの存在確認・読み込みのオーバーヘッドが存在しますから、以下に留意して使用する必要があります。
キャッシュヒット率を意識する
もしもキャッシュヒット率は1%などの場合は、むしろパフォーマンスが悪化することもあります。キャッシュヒット率は実際に計測も出来ますし、概算も可能ですから、キャッシュを利用するときは常に意識しておく必要があります。
例えば、
- 1日あたり1000回の関数コールが見込まれるが、引数のパターンが1億種類あり、均等に分布しているもの
- 1日あたり1000回の関数コールが見込まれ、引数のパターンが10種類程度のもの
だと、明らかに後者のほうがキャッシュヒット率が高そうです。
計算量を意識する
キャッシュは、あまりに軽い関数ではオーバーヘッドの分逆効果となることがあります。
function multiply(a, b) {
return a * b;
}
これは、引数(a,b)を受け取り、掛け算して返すだけの単純なプログラムです。このようなプログラムは、場合によってはキャッシュから値を取り出すよりも毎回計算させたほうが遥かに高速になることが多いのです。
メモリを意識する
キャッシュを無尽蔵に使うと、いくら現代のマシンスペックをもってしてもメモリが足りなくなってしまいます。世に出ているポピュラーなキャッシュライブラリは、多くの場合キャッシュの数や容量を制限できる機能を有しています。
事前計算を行う
計算が重く、チューニングできないし、1回目のコールでパフォーマンスを出さないといけない、という場合、事前計算や読み込みを行う戦略を立てるのは良い手段です。
バッチ処理
たとえば、1日分のデータを集計して、分析や請求に使いたい場合、データの量によっては、都度計算していると画面が表示されるまで数分待たなければならないこともあります。これは、ユーザーにとってはとても使えたものじゃありません。
その場合、「1日分のデータは翌日になると更新されない」という特性があるので、日付が変わったら、すぐにバッチ処理による事前計算を行っておくことで、実際にデータが必要になったときに計算しなくてよくなります。
難点は、バッチ処理にも膨大な計算コストが必要になるということと、バッチ処理が完了するまでは最新のデータが閲覧出来ないということです。
場合によっては、バッチ処理を並列化したり、事前計算すべき対象を絞ったりするなどの工夫も必要ですし、「日付が更新されたからといってすぐに最新の情報を閲覧できるわけではない」と予め通知するなど、ユーザーの期待値を上手くコントロールする必要も出てきます。
バックグラウンド計算
「投機的実行」などと呼ばれることもありますが、ユーザーの行動を予測して、事前にファイルの読み込みや計算を行っておく手法があります。
Webサイトでの高速化の例としては、imgタグのloading属性のlazyという値を設定したときに示す挙動がそれにあたります。これは、ブラウザをスクロールしていき、viewportとimgタグの位置関係がある基準に達すると画像の読み込みを始める、という、遅延読み込みの一種なのですが、「ユーザーがページをスクロールするということは、その画像を表示する可能性が高い」という理屈に基づいた読み込みになっています。
ほか、わかりやすい例として、3Dゲーム等では、エリアチェンジの範囲に近づいたときに次のエリアを読み込み始めてローディングの高速化を図るものも存在します。
これらは全て、ユーザーに見えない(意識させない)ように読み込み、計算を行っていることが特徴的で、バックグラウンド処理と呼ばれています。
おわりに
パフォーマンスチューニングの手法をいくつかご紹介しました。処理の高速化という観点では、単純に振る舞いを変えずに計算量を節約したり、事前計算、計算結果の再利用(キャッシュ)する以外にも、あえて振る舞いを少し変更することで大幅な改善を見込んだりしているものもあります。
考え方や工夫次第では大きな効果を見込める、奥の深い世界なので、是非オリジナルの手法を研究してみてください。
また、過度なパフォーマンスチューニングは、ユーザーにとって意味が薄いものとなる可能性があります。あくまで主役はユーザーなので、ユーザーに寄り添って改善を行っていきたいものですね。